Networks and Neuroscience
A network primer straight into a recent theory of developmental disorders. Strap in, kids.
A note: If you’re familiar with scale-free networks, the first half of this piece might be a bit boring. Skip to the second section, which discusses how network models are being used to advance our understanding of autism and other developmental disorders.
Scale-Free Networks
Here’s a series of dots. What’s the best way to connect them up?
Well, what if we just connect all of the dots?
That seems pretty good. If I want to travel between my dots I can just take the fastest route.
But it’s a bit messy. This system works well in Dotland, where there’s infinite electricity, multi-dimensional travel is possible, and Priti Patel became a yogi instead of going into politics. But there’s a lot of extraneous stuff going on.
If I want to go from A to C, I have lots of choices. Some of the choices are basically duplications, such as going directly from A to C and going from A, to B, to C. They’re also indistinguishable on this map, because the direct route currently utilises the infamous Dotland subways under B.
If we left the paradise of Dotland and replaced our lines (or edges) with footpaths, and our dots with different shops around a fictional town, suddenly the duplication matters. If we have to pay maintenance costs, we want to minimise the number of footpaths, while still allowing people to get from Al Capone’s Pizza Shop (A) to Carr’s Kebabs (C) as fast as possible.
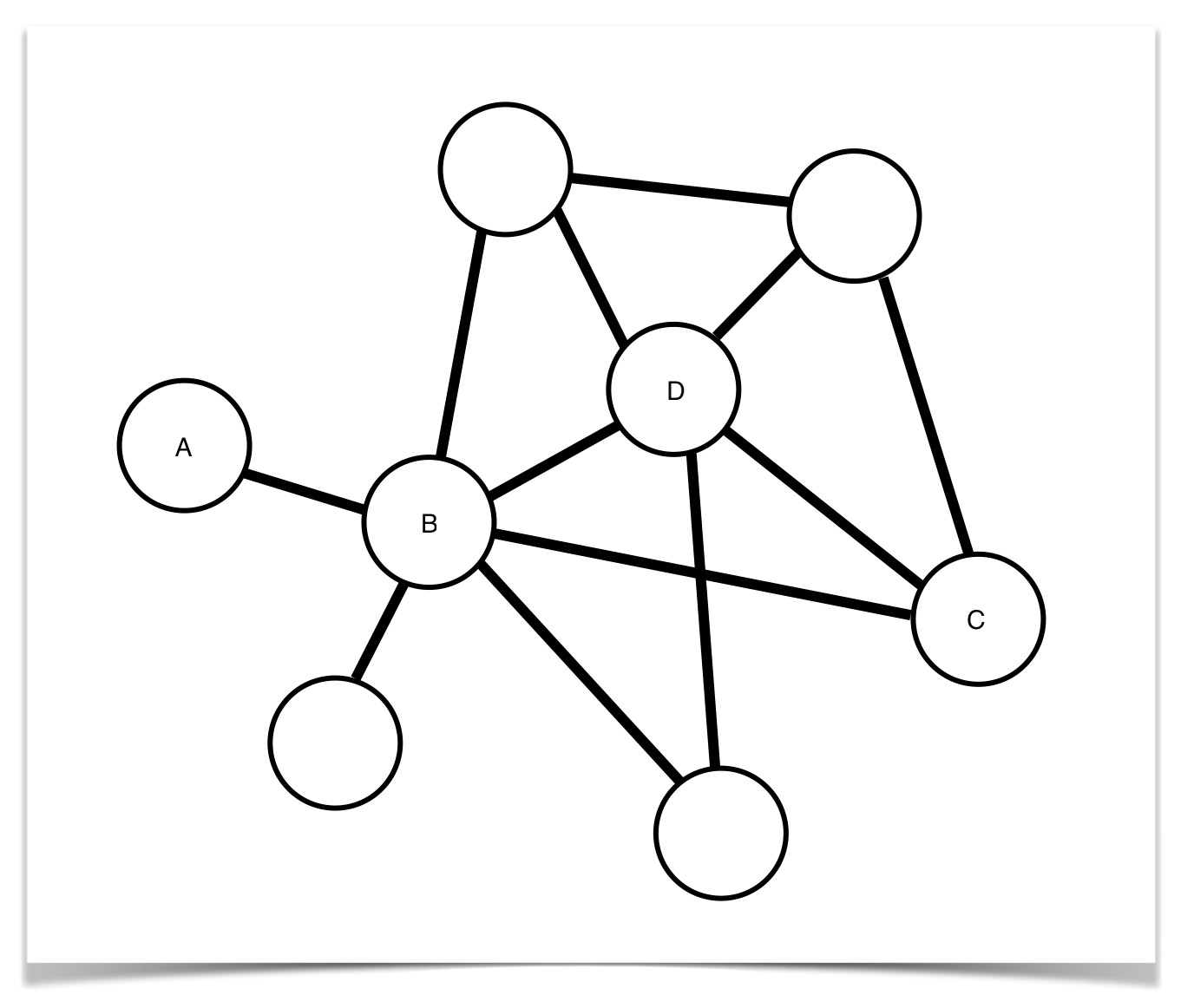
How about this?
A couple of things have happened here. We’ve cut down the number of connections, and instead now most footpaths run through two nodes, or hubs: B & D. And because they all run through those two hubs, that means we can make the footpaths wider and reinforce them (see how I’ve cunningly made the lines thicker), while saving money on footpath maintenance.
This is what is known as a scale-free network. The principle of a scale-free network is that most nodes have few connections, while there are a small number of very strongly connected hubs. Ignore the name for now, and just focus on the differences between the different structures.1 If we go back to the first, empty, network in Dotland, and we imagine adding each line at a time, how would each line get added? Here’s one where I’ve randomly added twelve lines:
This sucks. To get from Carr’s Kebabs (C) to the neighbouring Ed’s Discount Alcopop Shop (E), I have to cross the whole town, then take the winding backstreets, where I’ll probably be murdered by Alcopop addicts for my loose change.
One of the important insights of scale-free networks is that real networks don’t connect randomly. So, when you add in new lines, they usually connect to the most connected dots (or nodes). The implication of this work is that we usually don’t see the random networks as much in the real world, and instead, we’re better off modelling using scale-free networks.2
By now you’re probably thinking, looking at dots is tons of fun, but what’s the point of all this? The answer is that we can get a lot of insight into how things work using these sorts of methods. The other answer is that things in themselves often have a certain set of properties, but once they’re connected to other things, a totally different set of properties emerge.
I use the nonspecific ‘things’ intentionally, because nearly every conceivable thing can be modelled as a network if you really want to do so. Classic examples include traffic systems, Facebook friends, and that time Charlie from Sunny got to the bottom of the mailroom conspiracy.
Network Neuroscience
If we apply these principles to brains, all sorts of interesting things happen. Firstly, let’s turn our nice scale-free network into a brain network by adding a picture of a brain behind it:
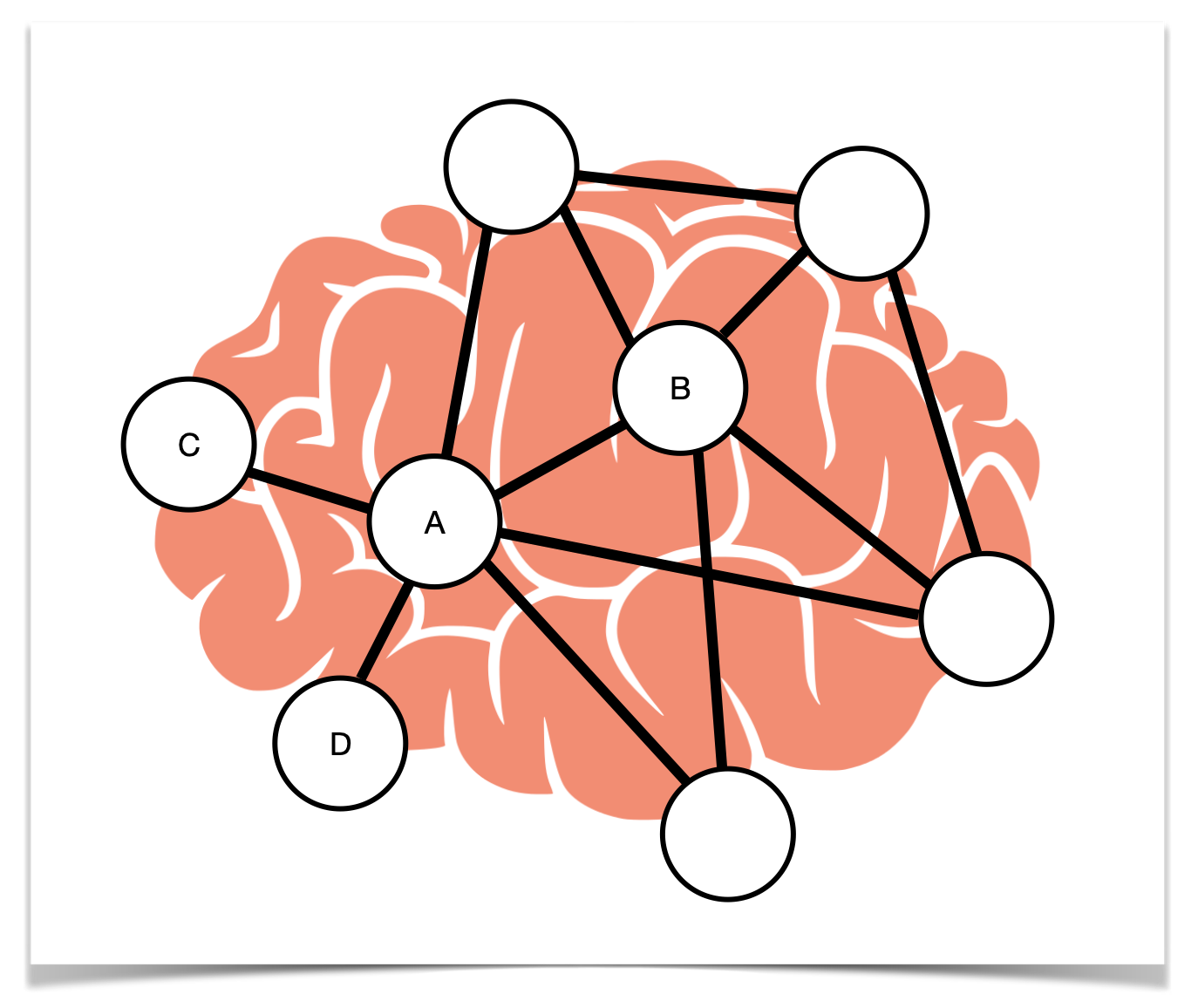
Great. So, one of the problems with developmental disorders like Autism Spectrum Disorder, or ADHD, or Aspergers, is that diagnoses are pretty variable. There seems to be a common set of symptoms, but the actual pathology is hard to pin down.
Siugzdaite et al. (2020) suggest that one of the main reasons for the difficulty tying symptomatology to pathology might be due to the way that brains networks are connected to each other.
They ran a huge study with 479 children (the average neuroscience sample size varies from around 20-30), and used a series of computational models to interpret the data.
They found that connectivity of different brain nodes and hubs was most predictive of whether children had developmental disorders. Kids with developmental disorders tended to have more distributed connections, with weaker hubs, while those without tended to have scale-free structures; networks with large, centralised hubs that dictate traffic.
As far as I can tell, Siugzdaite and friends are not specific on what these hubs actually represent, but Olaf Sporns has an answer here:
Several structural network studies of the human cerebral cortex have converged on a restricted set of regions that include the precuneus, anterior and posterior cingulate cortex, insula and portions of the superior frontal, temporal and lateral parietal cortex as putative network hubs.
The way they found this out was by running ‘attacks’ on the network, by disabling hubs at random (in a computer model, not in the children themselves, bloody ethics committees etc. etc.). For instance, imagine if we took out A in the brain network above. C & D are now unreachable, and left to fend for themselves.
In the counter-example, look at our random network:
Disabling A here is annoying, but we can still get everywhere. It’s just more circuitous. So the researchers were able to determine that there were different brain architectures because disabling hubs has a massive impact on children with highly efficient, hub-driven networks, but much less of an impact on children with more distributed networks.
But look at the structure of both brain networks! If the hubs are working, then the first network is much more efficient than the second one. It’s easier and faster to get around.
Siugzdaite clarifies this point:
The more central the hubs to a child’s brain organization, the milder or more specific the cognitive impairments. By contrast, where these hubs were less well embedded, children showed the more severe cognitive symptoms and learning difficulties.
So what does that mean more generally? Well, it suggests that any specific developmental diagnosis is less important than trying to determine the overall brain connectivity. To take a hypothetical, a child with autism and a child with Aspergers may have the same underlying brain structure, but a different connectivity map between different nodes. The emergent structure of this connectivity then generates two different sets of behaviour, resulting in the different diagnoses.
This study isn’t perfect by any means, and there’s a good review of it by Michael Thomas.
It also suffers from the usual neuroscience problem, which I’m going to call ‘WTFCATS?’ or ‘What the fuck causes all this shit?’3
Here’s Siugzdaite to elaborate:
Do local differences cause this greater integration to develop as a means of dynamic compensation over developmental time, or, does this integration vary across children regardless, making some more susceptible to the ongoing underdevelopment of specific regions?
All of this stuff can hopefully be tested (both Siugzdaite and Thomas think a similar longitudinal study would resolve a lot of questions), and network theories of systems are invaluable for getting towards understanding all manner of complicated problems.
With a better understanding of how the brain organises itself, we might be able to intervene and nudge those with developmental disorders towards a better brain architecture.
For some reason on Substack footnotes are glued to the bottom of the page, so I’m not going to do a Stuff I’ve Enjoyed section this time around, because it messes with the formatting.
It’s named after the “scale-free nature of power laws observed in the vicinity of phase transitions”.
This claim is subject to massive debate in the Network Science literature, and the actual prevalence of scale-free networks in the world is hotly contested. Here’s the case that says they aren’t very common. Here’s a response from Albert-László Barabási, who created the scale-free networks model with his partner, Réka Albert. There’s a humorous network-science based anecdote here, because the model they created is called the Barabási–Albert model, so it really looks like he invented a model and then named it after himself twice. One to tell the family.
Many prominent brain imaging techniques are notoriously bad for determining causation.